ビジネスの現場で『断固たる決意』を持つために、簡易的にExcelで統計処理を実行できるデータ分析ツールは大きな味方となってくれます。

3日回目の今回は次の２つについて触れていきます。

目次

1.順位と百分位数
2.共分散

順位と百分位数

これは対象データ内の個々の値に対して、データ内での順位と百分率で示された相対位置(相対順位)を表示してくれる機能です。

例えば実店舗を展開している企業の場合、各店舗の売上に対して順位付けと上位5割以上のラインがどこになるのか、ということを一発で示してくれます。

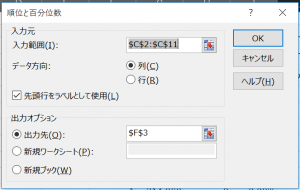
設定の流れとしては以下。
***************************************************************
１、「入力元 ＞ 入力範囲」に順位と百分位数を算出したいデータ群の範囲を指定。

※「ラベル」のチェックはデータの名称を定めたデータラベルが指定範囲に含められているかどうかを問うもの。

２、「出力オプション」にて算出データの出力先を指定。

***************************************************************

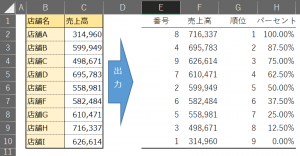
データサンプルと出力結果は下記のようになります。

出力結果において注意したい点としては、分析ツールの出力結果として値の対となる店舗名などをそのまま盛り込むことができないため、対象の値が何番目に位置していたのかという「番号」という列項目が出力されている点です。これを実際の店舗名などと付け合わせを行うには別途関数による処理が必要となります。

※左側が処理に使用したサンプルデータ、右側が分析ツールにより出力された結果。

※「順位」列に示されたランキング順に表示されている。パーセントでは対象となる店舗が全体の中で何％の位置にいるのかが示されている。

簡易的な処理ですが、優劣を判断するにはとても重要な機能です。

共分散

聞きなれない方も多いとは思いますが、相関係数同様、2変量の関係性を示す指標です。

共分散は下記のような性質を持ちます。

イメージとしても、正・負、また0に近いかどうかで関係性を示しているのは、相関係数と同じですよね。ただ、一点相関係数と異なるのは、-1～1の間で示されるといった基準値化が行われておらず、数値の大きさや単位によって出力される値が大きく変動してしまうため、関係性の強弱を判断することが難しいということです。

尚、数式的な意味合いでいうと、『2 組の対応するデータ間での、平均からの偏差の積の平均値』となります。

※相関係数はこの共分散を更に2 組の対応するデータの標準偏差の積で割ったもの。

通常、2変量間の関係性を示す際は相関係数の方が使いやすいですが、共分散は回帰分析などのその他分析手法においても、計算式に組み込まれているものとなっていますので、覚えておいても損はないと思います。

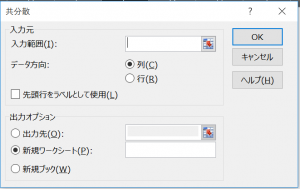
設定の流れとしては以下。
***************************************************************
１、「入力元 ＞ 入力範囲」に共分散を見たいデータ群の範囲を指定。
※「データ方向」は指定データ範囲が列(縦)方向に配置されているのか、行(横)方向に配置されているのかを指定。
※「先頭行をラベルとして使用」のチェックはデータの名称を定めたデータラベルが指定範囲に含められているかどうかを問うもの。

２、「出力オプション」にて算出データの出力先を指定。

***************************************************************

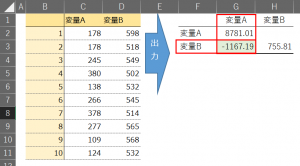
データサンプルと出力結果は下記のようになります。

※左側が処理に使用したサンプルデータ、右側が分析ツールにより出力された結果。

※赤枠で囲み色付けを行ったセルが変量Aと変量Bにおける共分散を示す。ここでは負の値となっているので、負の相関を持つと考えられる。

今回は以上です。